Parallella Examples

Performance is of paramount importance in parallel programming. The reason we are in the game of writing parallel programs is either to solve a problem faster than on a serial computer, or to solve a larger problem than could previously be done.
 
~D. Thiébaut, author
 Parallel Programming in C for the Transputer

Some developers buy a Parallella board because they already know parallel programming. They knew what to do with the device the moment they laid eyes on it. Others (like me) are relatively new to parallel programming. We see Parallella as an inexpensive tool for hands-on learning.

Starting Questions

A first-time Parallella user might ask questions like:

• How do you get Parallella up and running? Covered in the Parallella Quick Start Guide. Gotchas are included to save us time.

• What’s next? What can I do with Parallella that I can’t do with a single-core system?

To help answer the second set of questions, Adapteva gathered some examples that you can run on your own Parallella.

Community Examples on GitHub

The parallella-examples repo on GitHub is a great place to start. As of this writing, the examples include matrix multiplication, ray tracing, and Mandelbrot sets. Given the active nature of open source, more examples may appear by the time you read this. Future examples might be created by you!

Switching to TTY on Parallella

Some of the examples will not run on the Parallella’s Linux X Window desktop. Instead, TTY (teletype) mode is required. I will update this article when I find out why we need TTY. In the meantime, here’s how to switch to TTY mode and back on Parallella:

• Switch to TTY by pressing Ctrl + Alt + F2.

• The first time you switch to TTY, you will need to log in. Use the default Parallella credentials: login = linaro, password = linaro.

• Switch back to X Window by pressing Ctrl + Alt + F7.

Interesting observation: On my Parallella, pressing Ctrl + Alt + F[any number except 7] shifts the device to TTY mode. Only Ctrl + Alt + F7 switches it back to X Window.

Running the Mandelbrot Example

To run the Mandelbrot example, switch to TTY mode and then…

$ cd parallella-examples/mandelbrot

$ make     # You'll only need to run make once.

$ ./run.sh

You’ll see an animated graphic showing the Mandelbrot calculations in real time.

So, what’s a Mandelbrot set and why do we care?

About Mandelbrot Sets

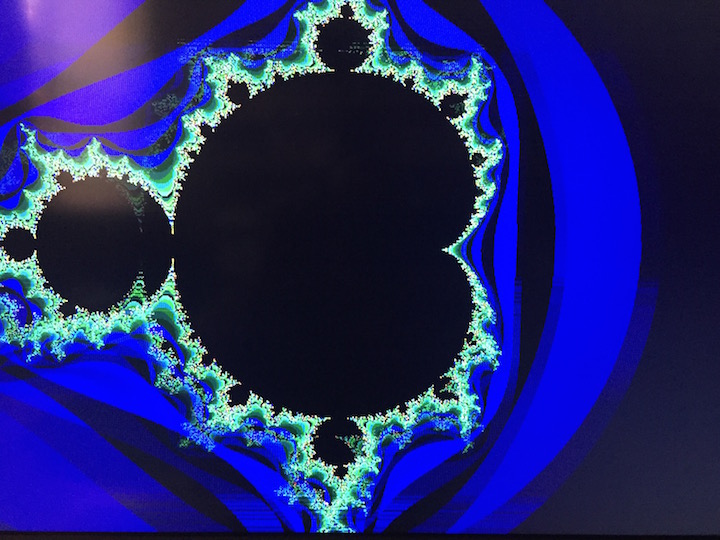
Clouds are not spheres, mountains are not cones, coastlines are not circles, and bark is not smooth, nor does lightning travel in a straight line.
 
~Benoit Mandelbrot

A Mandelbrot set is a group of numbers that displays a certain unusual property. Each member of the set is based on a calculation performed on the previous member, and an infinite number of members can be plotted within a finite area of a plane. Since humans are visual, we can easily recognize a Mandelbrot set that has been plotted on a graph, like the Mandelbrot diagram in this article.

For a 15-minute explanation of the Mandelbrot set, check out The Amazing Mandelbrot Set Tutorial. The video covers imaginary numbers, complex numbers, and iterative functions with just enough depth to explain how the Mandelbrot set gets generated.

A Mandelbrot algorithm designed for and executed on a parallel system will run faster than a similar algorithm running in serial. The algorithm and the code must be tailored for a parallel system in order for the advantage to be realized.

Other Parallella Examples

As of this writing, the other graphical programs in the parallella-examples repo can be run in a similar fashion. cd into the directory, run make, and then ./run.sh.

Next steps

Parallella is a learning tool. A learning lab. When we are learning, we ask questions like:

• How can we measure the difference in performance between serial and parallel versions of different algorithms?

• Why do the graphics-oriented examples require TTY mode?

• Scrot works on several single-board computers, including Parallella and Raspberry Pi. Why won’t Scrot work in TTY mode on Parallella?

• Once we get the graphics examples (like Mandelbrot and ray tracing) working in X Window, what’s the best way to record the on-screen animation? Holding a camera in front of the monitor will work, but it seems archaic.

And, the biggest questions of all:

• What can we do with Parallella that we cannot do with a single-core computer?

• How can we demonstrate the difference visually?